§ 5. Численное интегрирование обыкновенных дифференциальных уравнений

1. Задача Коши. Задача нахождения частного решения у = у(х) (y(x₀) = y₀) дифференциального уравнения y’ = f(x, y) называемая задачей Коши, может быть приближенно решена численными мето­дами.

 

М е т о д    Э й л е р а. Значения искомой функции у = у(х) на от­резке [x₀, X] находят по формуле

где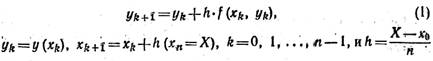                                                  

(шаг). По заданной предельной абсолютной погрешности ε начальный шаг вычислений h устанавливают с помощью неравенства h² < ε

 

М е т о д    Э й л е р а     c     и т е р а ц и я м и.   Для вычисления  значе­ний функции у = у(х) применяют формулу

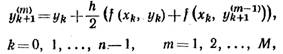(2)

где y⁽⁰⁾_k+1 = y_k+1 вычисляют по формуле (1). При каждом значении k вычисления продолжаются до выполнения неравенства

(3)

где ε — заданная предельная абсолютная погрешность. После этого полагают y_k+1 = = y^(m)_k+1 и переходят к нахождению следующего значения y_k+2 искомой функции. Если неравенство (3) не достигается, то уменьшают шаг h и выполняют все вычисления сначала. По

заданной предельной абсолютной погрешности ε начальный шаг вычислений h устанавливают с помощью неравенства h³ < ε. Апостериорная оценка точности выполняется при помощи правила Рунге-Ромберга (см. ниже)

 

М е т о д    Р у н г е - К у т т а. Значения искомой функции y = y(x) на отрезке [х₀, X] последовательно находят по формулам

  

где

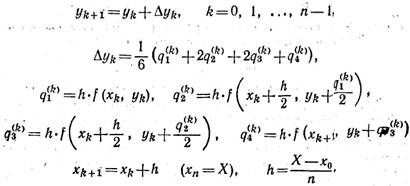(4)

 

 По заданной предельной абсолютной погрешности ε начальный шаг вычислений h устанавливают с помощью неравенства h⁴ < ε. Апостериорная оценка точности выполняется по правилу Рунге—Ромберга.

 

П р а в и л о    Р у н г е — Р о м б е р г а . Пусть у_k^(h) и у_2k^(2h) — значения искомой функции, полученные одним из указаний выше методов при шагах вычисления h и 2h соответственно, а ε — заданная абсо­лютная предельная погрешность Тогда считается, что достигнута заданная точность вычислений, если выполняется неравенство

(5)

при всех k и при s = 2, 3, 4 соответственно для методов Эйлера, Эйлера с итерациями и Рунге — Кутта. Решением задачи является функция .

 

Применяя указанное правило, последовательно вычисляют значения искомой функции с шагом 2h и с шагом h и сравнивают полученные результаты по формуле (5). Вычисления заканчивают, когда неравенство (5) выполняется при всех k.

 

 

2. Краевая задача для линейного уравнения. Краевая задача для линейного дифференциального уравнения

где р(к), q (х) и f(x) — некоторые непрерывные на отрезке [а, b] функции, состоит в нахождении его решения у = у (к), удовлетворяющего граничным условиям

где α₀, α₁, β₀, β₁, A, B  —постоянные   и |α₀| + |α₁| ¹ 0, | β₀| + | β₁| ¹ 0. Эта задача может быть решена численно методом конечных разностей, применяя который значения функции у= у(х) нахо­дят из системы линейных уравнений (n + 1)-гo порядка вида:

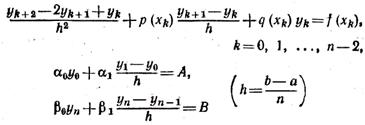(8)

с n + 1 неизвестными у₀, у₀, ..., у_n.