Теория линейных дифференциальных уравнений.

3. Линейные однородные уравнения. Уравнение вида

(5)

называется линейным однородным дифференциальным уравнением n-го порядка. Если известно какое-либо частное решение y₁(x) уравнения (5), то подстановка   y(x) = y₁(x) z(x) приводит- это уравнение к линейному уравнению относительно функции z(x), не содержащему явно эту функцию. Поэтому, полагая z’(x) = u(x), получим линейное однородное уравнение порядка n—1 относительно функции и(х).

 

Определителем Вронского (вронскианом) системы  функций y₁(x), y₂(x), …, y_n(x)  называется определитель

 

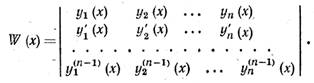Если система функций y₁(x), y₂(x), …, y_n(x) линейно зависима на интервале (а, b), то ее вронскиан равен нулю всюду на этом интервале. Если же хотя бы в одной точке x₀ Î (a, b) имеем W (х₀) ¹ 0, то система функций y₁(x), y₂(x), …, y_n(x) линейно независима на (а, b).

 

Всякая система из п линейно независимых решений y₁(x), y₂(x), …, y_n(x) уравнения (5) называется фундаментальной систе­мой решений этого уравнения. Вронскиан фундаментальной системы решений отличен от нуля на всем интервале, где эти решения опре­делены (см. задачу 9.304). Если известна фундаментальная система решений уравнения (5), то общее решение этого уравнения имеет вид

где C₁,  ..., С_п — произвольные постоянные.

 

4. Линейные неоднородные уравнения. Уравнение вида

(8)

в котором  f(x) ≠ 0, называется линейным неоднородным дифференциальным уравнением п-го порядка.

Общее решение уравнения (8) определяется формулой

y(x) = y0 (x) + ỹ(x)

(9)

где y₀ (x) — общее решение соответствующего однородного уравнения (5), а ỹ(x) — некоторое частное решение неоднородного уравнения (8).

 

Если известно общее решение y₀(x) =  C₁ y₁(x)+ …+ C_n y_n(x) соответствующего уравнению (8) однородного уравнения (5), то для

определения частного решения ỹ(x)  уравнения (8) можно воспользоваться методом Лагранжа вариации произвольных постоянных.

Именно, будем искать частное решение неоднородного уравнения (8) в виде  ỹ(x) = C₁ y₁(x)+ …+ C_n y_n(x), где от функций C₁(x), …, C_n(x) дополнительно потребуем, чтобы они удовлетворяли

условиям  для всех k=0, 1, ..., п —2 (где  ). Тогда  для функций C_ν (x), v=1,   2,  ..., п, получим систему уравнений

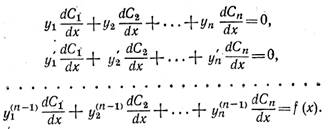(10)

 Определитель этой системы есть отличный от нуля вронскиан фундаментальной системы решений y₁(x), ..., у_п(х), поэтому система имеет единственное решение относительно

 

Если правая часть линейного неоднородного уравнения (8) есть сум­ма нескольких функций

и ỹ_i (x) (i=1, 2,  ..., r) — некоторые     частные   решения   уравнений  (i = 1,2,...,r)

соответственно, то сумма

есть некоторое частное решение уравнения (8) (п р и н ц и п     с у п е р ­ п о з и ц и и    р е ш е н и й).

 

5. Линейные однородные уравнения с постоянными коэффициентами. Общий вид линейного дифференциального уравнения порядка п с постоянными коэффициентами

(12)

                                         

где a_i (i = 1, 2, .. , n) — действительные постоянные. Уравнение

(13)

полученное заменой производных  y^(k) (k = 0, 1, …, n) искомой функции степенями λ^k, называется характеристическим уравнениемдля уравнения (12). Каждому действительному корню λ уравнения (13) кратности r соответствуют r линейно независимых решений уравне­ния (12):

а каждой паре комплексных корней λ = α ± iβ кратности s соответствуют s пар линейно независимых решений

Таким образом если характеристическое уравнение имеет k действительных корней λ₁ , …, λ_k кратностей r₁ , …, r_k и l пар комплексно сопряженных корней

кратностей s₁ , …,s_l   , то общее решение уравнения (12) Запишется в виде

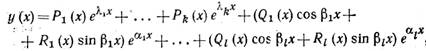(13)

 где Рν (х) — произвольный многочлен   степени  r_ν — 1, ν = 1, … , k, а Q_μ(x) и R_μ(x) —произвольные многочлены степени s_μ - 1, μ = 1, …, l

 

6. Линейные неоднородные уравнения с постоянными коэффициентами. Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами, т. е. уравнение вида

(15)

 

где a_i (i = 1, 2, …, n) — действительные постоянные, а f(x) ¹ o.

Согласно формуле (9) общее решение уравнения (15) записывается в виде y(x) = y₀(x) + ỹ(x), где y₀(x) —общее решение соответствующего однородного уравнения, а ỹ(x)—любое частное решение уравнения (15). Общее решение у₀(х) дается формулой (14). Для отыска­ния ỹ(x) в общем случае можно воспользоваться методом Лагранжа вариации произвольных постоянных (см. п. 4).

 

7. Дифференциальные уравнения Эйлера. Уравнение вида

где a_i (i=l, 2, ..., n) постоянные, есть частный случай линейного дифференциального уравнения с переменными коэффициентами и называется уравнением Эйлера. Введем новую независимую переменную t с помощью подстановки x = e^t (если х > 0) или подстановки x = -e^t (еcли х < 0). Пусть для определенности х > 0. Тогда    и т д., и уравнение Эйлера преобразуется в линейное уравнение с постоянными коэффициентами.

Уравнение вида

где а, b, a_i (i=1, 2, ..., п) — постоянные, приводится к линейному уравнению с постоянными коэффициентами подстановкой ax + b = e^t (в области ах + b > 0)

 

Решение однородного уравнения Эйлера

можно (при х > 0) искать в виде y = x^λ.

 

Подставляя выражения для y’, y”, …, y⁽ⁿ⁾ в однородное уравнение Эйлера, находим характеристическое уравнение для определения показателя степени λ При этом, если λ — действительный корень характеристического уравнения кратности r, то ему соответствуют r линейно независимых решений

а если α ± iβ — пара комплексных корней кратности s, то ей соответствуют

s пар линейно независимых решений

8. Краевые задачи в случае линейных дифференциальных уравнений. Во многих физических задачах приходится искать решение дифференциальных уравнений не по заданным начальным условиям, а по их значениям на концах интервала Такие задачи получили название краевых (граничных) задач. Общий вид краевых условий для интервала (a, b) в случае уравнении 2-го порядка таков:

                                                            (20)

где a₀, a , β₀, β₁ —одновременно не равные нулю заданные постоянные. Краевые условия называются однородными, если из того, что функции y₁(x) и y₂(x) удовлетворяют этим условиям, следует, что и их линейная комбинация  также удовлетворяет этим условиям. Краевые условия (20) при A = B = 0, очевидно, однородны.

Краевые задачи не всегда разрешимы. При решении краевой задачи сначала находится общее решение данного дифференциального уравнения, и из граничных условий получается система для определения значений постоянных  C₁, C₂, …, C_n , при которых из общего решения получается решение данной краевой задачи.