5. Линейные однородные уравнения с постоянными коэффициентами.
Общий вид линейного
дифференциального уравнения порядка п
с постоянными коэффициентами
|
|
(12) |
где ai (i = 1, 2, .. , n) — действительные
постоянные. Уравнение
|
|
(13) |
полученное
заменой производных y(k) (k = 0, 1, …, n) искомой функции степенями λk, называется
характеристическим уравнениемдля уравнения (12). Каждому действительному
корню λ уравнения (13) кратности
r соответствуют r линейно независимых решений уравнения (12):
![]()
а каждой паре
комплексных корней λ = α ± iβ кратности s соответствуют s пар линейно независимых решений
![]()
Таким образом если характеристическое уравнение имеет k действительных корней λ1 , …, λk кратностей r1 , …, rk
и l пар комплексно сопряженных корней ![]()
кратностей s1 , …,sl ![]() ,
то общее решение уравнения (12) Запишется в виде
,
то общее решение уравнения (12) Запишется в виде
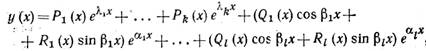 |
(14) |
6. Линейные неоднородные уравнения с постоянными коэффициентами. Рассмотрим линейное неоднородное
дифференциальное уравнение с постоянными коэффициентами, т. е. уравнение вида
|
|
(15) |
где ai (i = 1, 2, …, n) — действительные постоянные, а f(x) ¹ o.
Согласно
формуле (9) общее решение уравнения (15) записывается в виде y(x) = y0(x) + ỹ(x), где y0(x) —общее решение соответствующего
однородного уравнения, а ỹ(x)—любое частное решение уравнения (15). Общее решение у0(х) дается
формулой (14). Для отыскания ỹ(x)
в общем случае
можно воспользоваться методом Лагранжа вариации произвольных
постоянных (см. п. 4).