4. Линейные однородные  системы. Нормальная линейная однородная система n-го порядка имеет вид

 

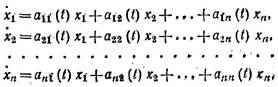(12)

 

или, в матричной форме,

(13)

где

 

 В области непрерывности коэффициентов a_ij(t), i, j = 1, …, n, система (12) удовлетворяет условиям теоремы существования и единственности решения задачи Коши.

 

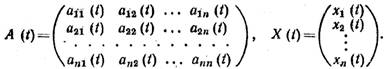
Фундаментальной системой решений системы (12) называется совокупность  произвольных п линейно независимых решений

Если X_k (t),k = 1, 2, …, n ,— фундаментальная система решений системы (12), то общее решение имеет вид , где

 —произвольные постоянные. Интегрирование системы (12) обычно проводится методом исключения (см. пример 3).

В частном случае систем с постоянными коэффициентами, когда матрица A (t) в правой части (13) не зависит от t, для отыскания фундаментальной системы решений X_k (t),k = 1, 2, …, n, могут быть использованы методы линейной алгебры.

Из характеристического уравнения

det (A - λE) = 0

(14)

           

находятся различные корни λ₁, λ₂, … λ_s  и для всякого корня λ (с учетом его кратности) определяется соответствующее ему частное решение X^(λ)(t). Общее решение системы имеет вид

(15)

При этом возможны следующие случаи:

а) λ — действительный корень кратности 1. Тогда

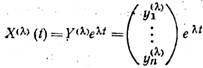
где Y^(λ), — собственный вектор матрицы А, соответствующий .собственному значению λ (т.е. AY^(λ) = λY^(λ), Y^(λ) ¹ 0)

 

б) λ — комплексный корень кратности 1. Тогда корнем характеристического уравнения (14) является также сопряженное с λ число` λ.

Вместо комплексных частных решений X^(λ)(t) и X^(`λ)(t) следует взять действительные частные решения X₁^(λ)(t) = Re X^(λ)(t) и X₂^(λ)(t) = Im X^(λ)(t).

 

в) λ, — корень кратности r≥ 2. Соответствующее этому корню решение системы (13) ищется в виде вектора

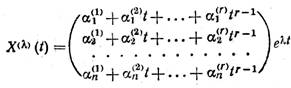(16)

 

коэффициенты которого α_i^(j), i = 1, …, n; j = 1, … r, определяются из системы линейных уравнений, получающейся приравниванием коэффициентов при одинаковых степенях t в результате подстановки вектора (16) в исходную систему (13)

 

5. Линейные неоднородные системы. Нормальная линейная неоднородная система дифференциальных уравнений имеет вид

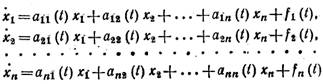(17)

 

где по крайней мере одна из функций f_k(t) не равна тождественно нулю. В матричной форме система (17) имеет вид

(18)

где F(t) = (f₁(t), f₂(t), … f_n(t))^T. Интегрирование системы (17) можно проводить методом исключения (см. пример 3), однако иногда предпочтительнее найти предварительно решение X₀(t) соответствующей (18) однородной системы

(19)

и какое-либо частное решение   системы (18). Тогда общее решение системы (18) имеет вид

(20)

 

Если известна фундаментальная система X_k (t), k = 1, 2, …, n, решений однородной системы (19), то общее решение X(t) можно найти

методом вариации произвольных постоянных. Именно, полагая

(21)

 

определяем функции C_k(t) подстановкой (21) в систему (18). Учитывая при этом равенства

приходим к системе уравнений относительно Ċ_k(t):

(22)

Из этой системы находим Ċ_k(t) = φ_k(t) и, интегрируя, получаем функции C_k(t) с точностью до произвольных постоянных. Подставляя их в

(21), получаем искомое общее решение неоднородной системы (18).

 

Если коэффициенты а_ij(t) системы (17) постоянны, т. е. , а_ij(t) = а_ij, i, j = 1, …, n, а функции f_i(t) имеют вид произведений

(23)

где P(t) и Q(t) — многочлены, то частное решение можно найти методом неопределенных коэффициентов, записав  в виде, аналогичном (23), с учетом совпадения или несовпадения чисел α ± iβ с корнями характеристического уравнения.

Следует иметь в виду, что если k — наибольшая степень многочленов Р (t) и Q (t) в (23) и λ = α ± iβ — корень кратности r характеристического уравнения, то частное решение  ищется в виде

.
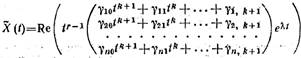