Ряды с комплексными членами. Разложение аналитической функции в ряд Тейлора

1. Область сходимости и свойства степенных рядов

Ряд

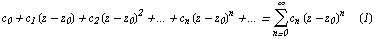
Называется степенным по степеням 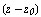. В частности ряд

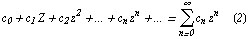
Является степенным по степеням z. С помощу замены 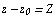ряд (1) сводится к ряду (2).

Теорема Абеля. Если степенной ряд (2) сходится в точке 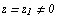, то он абсолютно сходится для всех z таких что , причем сходимость будет равномерной в любом замкнутом круге 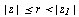. Если же ряд (2) расходится в точке 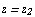, то он расходится и для всех z таких, что .

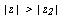Из теоремы Абеля следует, что областью сходимости степенного ряда является круг с центром в начале координат (с центром в точке 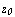), радиус которого может быть определен применением либо признаком Даламбера, либо признаком Коши, т.е. из условий

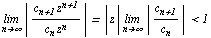
или

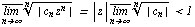
Отсюда для вычисления радиуса R круга сходимости получаем соотношения

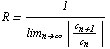или

2.Разложение функций в ряд Тейлора.

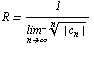
Имеет место следующая Теорема Тейлора. Функция 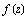, аналитическая в круге 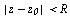, однозначно представима в этом круге своим рядом Teaлора

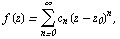
коэффициенты которого определяются по формулам

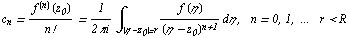
Следствие. Если функция 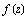аналитична в области D и 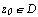, то в круг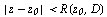е , где 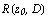- наименьшее расстояние от точки 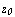до границы области D или до ближайшей точки 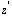, в которой 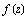не аналитична, 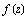может быть представлена в виде степенного ряда:

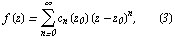
коэффициенты которого определяются по формулам

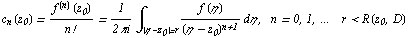
Если 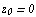, то ряд Тейлора называют также рядом Маклорена.

3.Применение степенных рядов

Найти число е с точностью до .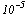

Подставив х = 1 в разложение функции 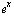, имеем

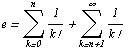
Оценим остаток

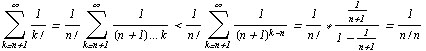
Следовательно, равенство

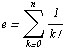
имеет предельную абсолютную погрешность, равную 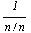. Найдем п, для которого 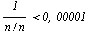, или 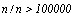. Получаем 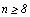. Вычисляя 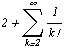и округляя, находим ответ с требуемой точностью е = 2,71828.