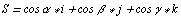 - единичный
вектор данного направления
- единичный
вектор данного направления 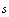 ,
, 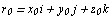 - радиус-вектор
точки
- радиус-вектор
точки 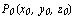 . Производная скалярного поля
. Производная скалярного поля 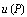 в точке
в точке 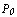 по направлению
по направлению 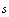 , обозначаемая
через
, обозначаемая
через 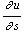 , определяется соотношением
, определяется соотношением |
|
Литературная справка |
Пусть 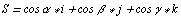 - единичный
вектор данного направления
- единичный
вектор данного направления 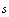 ,
, 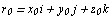 - радиус-вектор
точки
- радиус-вектор
точки 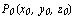 . Производная скалярного поля
. Производная скалярного поля 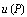 в точке
в точке 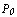 по направлению
по направлению 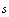 , обозначаемая
через
, обозначаемая
через 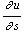 , определяется соотношением
, определяется соотношением
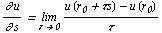
и характеризует скорость изменения функции 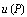 в направлении
в направлении 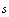 . Производная
. Производная 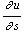 вычисляется по формуле
вычисляется по формуле
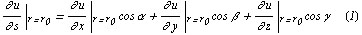
Градиентом скалярного поля 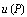 , обозначаемым символом
, обозначаемым символом 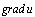 и, называется вектор, проекциями которого на координатные оси являются соответствующие частные производные функции
и, называется вектор, проекциями которого на координатные оси являются соответствующие частные производные функции 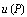 , т. е.
, т. е.
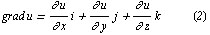
Аналогично определяется производная по направлению и градиент для n-мерных скалярных полей.
Векторное поле 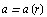 называется потенциальным, если вектор поля
называется потенциальным, если вектор поля 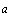 является градиентом некоторой скалярной функции
является градиентом некоторой скалярной функции 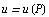 :
:
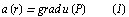
Функцию 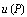 в этом случае называют потенциалом векторного поля. Необходимым и достаточным условием потенциальности дважды дифференцируемого в односвязной области поля
в этом случае называют потенциалом векторного поля. Необходимым и достаточным условием потенциальности дважды дифференцируемого в односвязной области поля 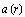 является равенство нулю вихря этого поля:
является равенство нулю вихря этого поля:
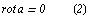
Проверить, что вихрь трехмерного векторного поля 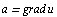 тождественно равен нулю (функцию
тождественно равен нулю (функцию 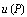 предполагаем дважды дифференцируемой).
предполагаем дважды дифференцируемой).
Так как 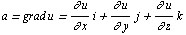 то, учитывая равенство смешанных производных 2-го порядка, получаем
то, учитывая равенство смешанных производных 2-го порядка, получаем
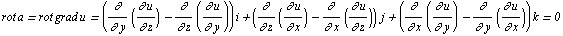
1. В области непрёрывности потенциала поля линейный интеграл от вектора поля, взятый между двумя точками поля не зависит от пути интегрирования и равен разности значений потенциала поля в конце и начале пути интегрирования
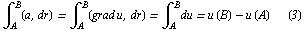
(использована легко проверяемая формула 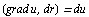 )
)
2. Циркуляция вектора поля по любому замкнутому контуру, целиком лежащему в области непрерывности поля, равна нулю
3. Если поле 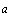 потенциально, то потенциал поля
потенциально, то потенциал поля 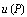 в произвольной точке
в произвольной точке 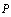 может быть вычислен по формуле (3):
может быть вычислен по формуле (3):
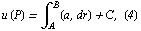
причем 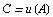 что легко получается подстановкой в (4) вместо переменной точки
что легко получается подстановкой в (4) вместо переменной точки 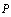 фиксированной точки
фиксированной точки 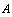 .
.
Для вычисления интеграла (4) можно выбрать любой путь
- проще всего в качестве такого пути выбрать ломаную со звеньями, параллельными
осям координат, соединяющую точки 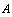 и
и 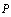 .
За точку
.
За точку 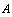 удобно принимать начало координат (если оно лежит
в области непрерывности поля).
удобно принимать начало координат (если оно лежит
в области непрерывности поля).