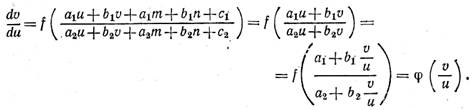3. Уравнения  с   разделяющимися   переменными.   Пусть  в уравнении

 

y' = f(x, y)

функция f (x, у) может быть разложена на множители, каждый из которых зависит только от одной переменной: f(x,y) = f₁ (x) f₂ (у), или в уравнении

M(x, y)dx + N(x, y)dy =0

коэффициенты при dх и dy представляются в виде М (х, у)—M₁ (x) М₂(у), N (x, y) = N₁ (x) N₂ (у). Путем деления соответственно на f₂ (у) и на n₁ (х) М₂ (у) эти уравнения приводятся соответственно к виду

Интегрируя левые части этих уравнений по х, а правые по у, приходим в каждом из них к общему интегралу исходного дифференциального уравнения.

 

Если в уравнении с разделяющимися переменными у’ = f₁(x)f₂(y) функция f₂(у) имеет действительный корень y₀, т. е. если f₂(y₀)=0, то функция у(х) = у₀ является решением уравнения (в чем легко убедиться непосредственной подстановкой). При делении обеих частей этого уравнения на f₂ (y) (при разделении переменных) решение y(х) = y₀ может быть потеряно.

 

Аналогично,   при   интегрировании   уравнения m₁ (x) М₂(у)dx + N₁ (x) N₂ (у)dy = 0 могут быть потеряны интегральные кривые х(у) = х₀ и у(х)=у₀, где х₀ — действительный корень уравнения N₁(x) = 0, у₀ — действительный корень уравнения M₂(y) = 0.

 

Поэтому, получив указанным выше методом разделения переменных общий интеграл уравнения, надо проверить, входят ли в его состав (при подходящих числовых значениях параметра С) упомяну­тые частные решения. Если входят, то потери решений нет. Если не входят, то их следует включить в состав интеграла.

 

 

 

4. Однородные   уравнения.   Дифференциальное   уравнение   1-го порядка  называется  однородным,  если  его   можно  привести к виду

(4)

или к виду

М(х, y)dx+N(x, y)dy = 0,

(5)

где  М (х,  у)  и  N (х, у) — однородные функции одного порядка, т. е. существует такое k Î Z, что тождественно относительно х, у и t ¹ 0.

С  помощью   подстановки   у/х = и(х) однородные уравнения (4) и (5) преобразуются в уравнения с разделяющимися переменными.

 

Дифференциальные уравнения вида

(6)

в случае приводятся к однородным уравнениям с помощью замены переменных

где т и п находятся из системы уравнений

Поскольку   здесь  dx = du, dy = dv_} то уравнение (6) преобразуется к виду  (4) относительно функции v (u):

Если в уравнении  и, следовательно, , то оно примет вид

Подстановкой  это уравнение преобразуется к урав­нению с разделяющимися переменными.

 

 

5. Линейные уравнения. Дифференциальное уравнение 1-го порядка называется линейным, если оно содержит у и у' в первой степени, т. е. имеет вид

(7)

                                                           

При Q (х) º 0 уравнение (7) принимает вид

у' = Р(х)у

и называется линейным однородным. Оно является уравнением с раз­деляющимися переменными, и его общее решение имеет вид

(8)

где  С—произвольная  постоянная,   а  — одна из   первообразных функции Р (х).

 

Интегрирование линейного неоднородного уравнения (7) можно провести одним из следующих методов.

 

   а) М е т о д   в а р и а ц и и   постоянной.   Будем   искать   решение уравнения (7) в виде

(9)

                                     

который получается из (8), если заменить постоянную С на функ­цию С (x). Подставляя выражение (9) в уравнение (7), получим для неизвестной функции С (х) уравнение с разделяющимися переменными:

Его общее решение:

 

где С—произвольная   постоянная,   а — одна   из

первообразных. Подставляя полученное выражение для С (х) в формулу (9), находим общее решение уравнения (7):

(10)

   б) М е т о д    п о д с т а н о в к и. Положим у(х) = и(х) v(х).   Тогда уравнение (7) приводится к виду

(11)

Выберем функцию и (х) так, чтобы первая скобка в левой части уравнения (11) обратилась в нуль. Для этого интегрируем уравнение с разделяющимися переменными

и выбираем какое-либо частное его решение и — и₁(х). Подставляя функцию и₁(х) вместо и в левую часть уравнения (11), получаем уравнение с разделяющимися переменными относительно функции v (х):

Находим общее решение этого уравнения v = v(x,C). Перемножая найденные функции и₁(х) и v(x, С), получаем общее решение урав­нения (7):

 

 

6. Уравнение Бернулли. Уравнением Бернулли называется дифференциальное уравнение 1-го порядка вида

(13)

где  (при   m = 0   уравнение   (13)   является  линейным, а при т=1—уравнением с разделяющимися переменными).

 

Так же, как и линейное, уравнение Бернулли можно проинтегрировать с помощью подстановки y = uv или свести к линейному уравнению с помощью подстановки  Следует учесть, что при m > 1 может быть потеряно решение y = 0.

 

 

7. Уравнения   в   полных    дифференциалах.    Дифференциальное уравнение 1-го порядка вида

(15)

называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции U (х, у), т. е.

Для того чтобы уравнение (15) было уравнением в полных диф­ференциалах, необходимо и  достаточно, чтобы  выполнялось  условие

(16)

Если  уравнение (15)   есть уравнение в полных   дифференциалах, то оно может быть записано в виде

dU (x, y) = 0

Общий интеграл этого уравнения:

U (x, y) = C,

где С—произвольная постоянная.

 

Функция U (х, у) может быть найдена следующим образом. Инте­грируя равенство  по  х при фиксированном у и  замечая, что произвольная постоянная в этом случае может зависеть от у, имеем

(17)

Затем из равенства

находим функцию j (у), подставив которую в (17), получим функцию U (х, у).

Очевидно, что искомая функция U (х, у) определена с точностью до произвольной аддитивной постоянной. Для записи общего интеграла исходного уравнения достаточно выбрать одну из функций получаемого семейства.

Другой метод отыскания функции U (х, у) состоит в вычислении криволинейного интеграла 2-го рода (см. гл. 10, § 2, 4):

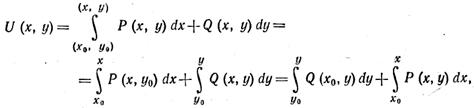
где точки М₀ (x₀, y₀) и М (х, у) и путь интегрирования лежат в области непрерывности функций Р (х, у) и Q (х, у) и их частных производных, причем М₀ (х₀, y₀ )— некоторая фиксированная точка.

 

 

9. Уравнения, не разрешенные относительно производной. Пусть дифференциальное уравнение F (х, у, y') = 0 разрешимо либо относительно искомой функции, т. е. имеет вид

y = f(x,y'),

(20)

                                                             

либо относительно аргумента, т. е. записывается в виде

х = f(y,y'),

(21)

Тогда оно интегрируется путем введения параметра р = у'. Уравнения (20) и (21) переходят в алгебраические уравнения, дифференцируя которые соответственно по х или по у, получим системы уравнений

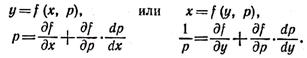
Из этих систем находится соответственно общее решение уравнения (20) или (21) в явном или параметрическом виде.

Пример 15. Решить уравнение

y = у'2+ху' - х.

Введем параметр р=у'. Тогда

y = р2+х(р-1).

(22)

                                                         

Дифференцируя это равенство по х, получим

или

Запишем последнее уравнение в форме

Это линейное уравнение, его общее решение:

x = CeP – 2(p + 1).

(23)

                                                

Подставляя выражение (23) в формулу (22), получим

y = CeP (p - 1) – p2 + 2

(24)

                                                 

Система соотношений (23) и (24) определяет общее решение исходного уравнения в параметрической форме:

 решение:

x = CeP – 2(p + 1),   y = CeP (p - 1) – p² + 2.