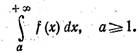2. Абсолютная и условная сходимость. Признаки
абсолютной сходимости.
Ряд (1) называется абсолютно сходящимся, если
сходится ряд из модулей членов этого ряда, т. е. сходится ряд
Если
ряд (1) сходится, а ряд (3) расходится,
то ряд (1) называется условно сходящимся.
Признак сравнения
рядов. Если члены ряда
(1) для всех n> n0 (N0 ≥ 1) удовлетворяют условию | иn | ≤ bn, причем ряд 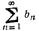 сходится,
то ряд (1) сходится
абсолютно.
сходится,
то ряд (1) сходится
абсолютно.
Если же для n > N1 члены ряда (1)
удовлетворяют условию 0 < сn ≤ |иn| , причем
ряд
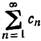 расходится, то ряд
(3) расходится, т. е, ряд (1) не сходится абсолютно.
расходится, то ряд
(3) расходится, т. е, ряд (1) не сходится абсолютно.
На
практике более эффективным оказывается следующий
Предельный
признак сравнения.
Если ряд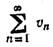 сходится
абсолютно и существует
сходится
абсолютно и существует
конечный предел 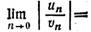
 ,то ряд (1)
также сходится абсолютно. Если же члены рядов иn и vn — действительные положительные
числа и
,то ряд (1)
также сходится абсолютно. Если же члены рядов иn и vn — действительные положительные
числа и
то
ряды  либо оба сходятся, либо оба расходятся
либо оба сходятся, либо оба расходятся
Признак Даламбера. Если члены ряда (1) таковы, что существует
конечный предел
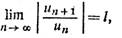
то при 0 ≤ l ≤ 1 ряд
(1) сходится абсолютно, при l > 1— расходится, а при l=1 требуется дополнительное исследование.
Признак
Коши. Пусть 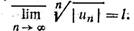 Тогда, если
Тогда, если
0
≤ l ≤
1, то ряд (1) сходится абсолютно, если l > 1— ряд (1) расходится, а при
l=1 требуется дополнительное исследование.
При
использовании признака Коши бывает полезна следующая
формула Стирлинга:
Интегральный
признак Коши.
Пусть функция f(x) положительна и монотонна при х ≥ 1, и пусть для всех nÎ N имеет место равенство f(n) = |un|. Тогда числовой ряд (3) сходится (т. е. ряд (1) сходится
абсолютно) или расходится одновременно с несобственным интегралом