2.   Разложение  функций   в ряд Тейлора. Имеет место следующая Теорема   Тейлора.   Функция  f (z),  аналитическая  в круге |z—z₀| < R, однозначно представима в этом, круге своим рядом Тейлора

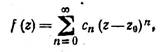коэффициенты которого определяются по формулам ¹)

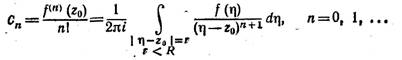
¹) Здесь и далее для записи криволинейных интегралов по замкнутому контуру (контурных интегралов) мы используем обычный знак интеграла.

 

 

Следствие. Если функция f (z) аналитична в области D и z₀ Î D , то в круге | z < z₀ | < R (z₀, D), где R (z₀, D) — наименьшее расстояние от точки z₀ до границы области D или до ближайшей точки z', в которой f (z) не аналитична, f (z) может быть представлена в виде степенного ряда

(3)

 

коэффициенты которого определяются по формулам

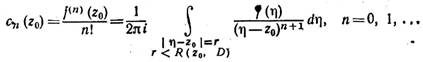
Если  z₀ = 0, то ряд Тейлора называют также рядом Маклорена.

Замечание. Если рассматривать ряд Тейлора функции f (х) действительной переменной, т. е. ряд

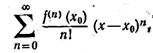то для справедливости равенства (3) (при z=х и z₀ = х₀) необходимо и достаточно, чтобы остаточный член формулы Тейлора R_n (х) стремился к нулю при п® ¥. Остаточный член может быть записан, например, в форме Лагранжа

или в форме Коши

или в какой-либо другой форме.

 

При   решении многих задач рекомендуется пользоваться следую­щими разложениями элементарных функций.

(в случае, когда  a = mÎ N  функция (1+z )^m   раскладывается по биному Ньютона в многочлен, причем разложение имеет место во всей плоскости).

ж) при a = -1 из е) получаем бесконечную геометрическую прогрессию со знаменателем —z